Review of Modern physics Volume 29 Number 3 July 1957

Negative mass in general relativity

H. Bondi

King’s College, University of London, London England

Traduction : J. Fric qui endosse la responsabilité des erreurs que sa traduction aurait pu introduire.

Masses négatives en Relativité Générale

1

Même si certains arguments associés à la masse négative sont plutôt élémentaires et bien connus, il est cependant intéressant de bien préciser ce que nous entendons sous ce vocable.

De prime abord, sans se référer à une théorie, nous pouvons distinguer trois types de masses définies par la mesure qu’on en fait : masse inertielle, masse gravitationnelle passive, masse gravitationnelle active. La masse inertielle est le coefficient qui intervient ( et qui est défini par) dans la seconde loi de Newton ( f = m.a) , la force « f » devant être de nature non gravitationnelle ( électromagnétique par exemple) pour s’assurer de l’indépendance des masses ; la masse passive est celle sur laquelle le champ gravitationnel agit ( couplage avec le champ), définie par f = -m.gradV; la masse active est celle qui est la source du champ gravitationnel et est donc celle qui intervient dans l’équation de Poisson et la loi de Gauss.

En physique Newtonienne la loi de l’action et de la réaction implique l’égalité des masses gravitationnelles actives et passives, mais leur égalité avec la masse inertielle est un constat empirique distinct. Le signe de ces masses peut prendre n’importe quelle valeur et c’est un autre fait empirique qu’on le considère toujours positif. Si on ne prend pas en compte ce dernier fait, alors quatre cas sont possibles.

(i) Toutes les masses sont positives : c’est le cas classique.

(ii) La masse inertielle est négative, les masses gravitationnelles sont positives. Un corps fait de telle matière va se comporter à l’inverse du cas standard lorsque soumis à toutes les forces quelles que soient leur nature, mais va générer des forces gravitationnelles classiques.

(iii) Masse inertielle positive, masses gravitationnelles négatives. Dans ce cas, les forces non gravitationnelles vont avoir le comportement habituel, mais si on considère les interactions gravitationnelles entre ces masses et les masses de type (i), c'est-à-dire positives, on a une loi de coulomb «  inversée ». Les masses de même nature (deux masses positives entre elles ou deux masses négatives entre elles) s’attirent, les masses de nature différentes (une masse négative en interaction avec une masse positive) se repoussent

(iv) Toutes les masses sont négatives. On va arriver à une combinaison de (ii) et (iii). Un corps fait de cette matière va se comporter à l’inverse du cas classique pour les forces non gravitationnelles, va se comporter comme la matière ordinaire vis-à-vis des forces gravitationnelles, mais va générer des champs gravitationnels répulsifs.

En Relativité la situation est différente. Le principe d’équivalence est inhérent à la théorie. Donc, le rapport entre la masse inertielle et la masse gravitationnelle passive est le même pour tous les corps. La relation entre la masse passive et la masse active n’est pas contrainte par quoi que ce soit comme la troisième loi de Newton, car ceci impliquerait des intégrales sur des régions étendues de l’espace temps qui ne possèdent pas le caractère tensoriel requis.

Pas mal de travaux ont été réalisés qui montrent que la relation est plutôt compliquée.

Tant que la Relativité est considérée comme une pure théorie de la gravitation, les masses passives et actives, en fait, n’apparaissent pas.

La masse gravitationnelle active apparaît, comme une constante d’intégration, pour la première fois dans la solution de Schwarzschild. Si cette constante est considérée positive, alors les particules de test, vont, en première approximation, suivre des orbites Newtoniennes correspondantes à l’attraction gravitationnelle du corps central. Si, cependant, on prend cette constante négative, les particules de test vont décrire des orbites qui correspondent à un cas «  Newtonien , mais répulsif. Remarquons que dans le premier cas, tous les corps sont attirés, dans le second tous les corps sont repoussés.

Quittons le problème à un corps et intéressons nous au problème à deux corps, où une situation peu commune se produit.

Supposons un corps de masse négative et un corps de masse positive séparés dans l’espace vide.

Alors, en utilisant le langage de l’approximation Newtonienne, le corps positif va attirer le corps négatif (car il attire tous les corps), tandis que le corps négatif va repousser le corps positif (car il repousse tous les corps). Si le mouvement ne se produit que sur la ligne des centres, alors on peut escompter que la paire va s’éloigner avec une accélération constante.

Ce résultat plutôt surprenant, nécessite manifestement confirmation par modélisation dans le cadre de la Relativité générale.

2

Les systèmes uniformément accélérés sont bien connus en Relativité générale ( et Restreinte), mais cela n’est pas inutile de rappeler brièvement les propriétés principales de tels systèmes.

Le concept d’accélération uniforme classique, peut être généralisé en Relativité Restreinte de différentes façons, mais l’une d’entre elles fondée sur la stationnarité est d’une importance particulière.

Le système est décrit dans ce cas par l’équation = constante.

( Le système est unidimensionnel en espace, est le temps)

Les orbites de toutes les particules dans le plan associé, forment un système d’hyperboles d’asymptotes fixes.

Ces particules ont toutes une accélération uniforme, dans le sens où le mouvement de chaque particule , du point de vue de l’autre est constant dans le temps.

Cependant, alors que l’accélération est uniforme en chaque point elle est différente en différent points.

En gros, plus la trajectoire de la particule passe près de l’origine plus l’accélération est grande.

La caractéristique remarquable de ce système est sa stationnarité.

Si chaque particule héberge un observateur mesurant la distance à une autre particule suivant le même mouvement (la trajectoire ?), il va trouver que cette distance ne varie pas dans le temps, bien que pour un observateur fixe , lui et l’autre particule ont des accélérations différentes.

La métrique de Minkowski habituelle peut être transformée en celle associée à un référentiel uniformément accéléré par la transformation

Ceci donne la métrique ds² = z²dt²-dx²-dy²-dz².

Il est clair que cette métrique ne décrit pas tout l’espace, mais est bornée par des asymptotes qui se comportent comme des horizons, en conséquence la métrique ne couvre qu’un quart de l’espace temps ( Fig 1)

Maintenant attachons nous à construire le modèle correspondant à deux corps de masses de signe opposé, en Relativité Générale.

Utilisons le référentiel uniformément accéléré et plaçons y deux corps de masses finies de signe de masse opposés. Dans le référentiel uniformément accéléré, le système va être à symétrie axiale, nous pouvons donc utiliser la métrique de Weyl et Levi Civita

Dans cette métrique, nous avons, dans le vide,

où satisfont

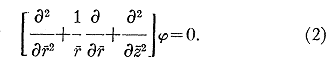
L’opérateur décrit en (2) sera noté

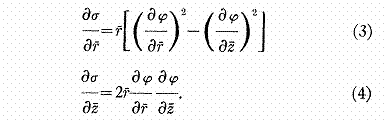
Il est bien connu, qu’on associe à cette métrique une condition de cohérence. Dans notre contexte, nous allons l’exprimer sous une forme légèrement différente de la forme usuelle.

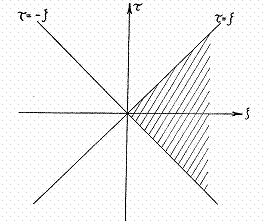
Fig 1. La région hachurée à droite est associée au demi espace z>=0 et aussi à l’espace entier

Pour toute trajectoire fermée dans le vide (même incluant une région non vide) de (3) et (4) nous tirons

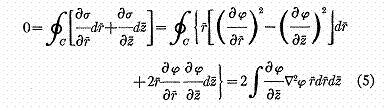
du théorème de divergence, l’intégrale étant prise à travers la partie du plan méridien délimité par la courbe C.

On a supposé ici que la métrique avait la forme (1) dans toute la région bien qu’elle ne satisfait pas forcément les équations (2) (3) et (4).

La métrique (1) n’est pas en fait la métrique la plus générale pour une région statique à symétrie axiale, non vide mais elle est suffisamment générale pour le modèle que nous nous proposons de construire.

Il est facile de montrer que :

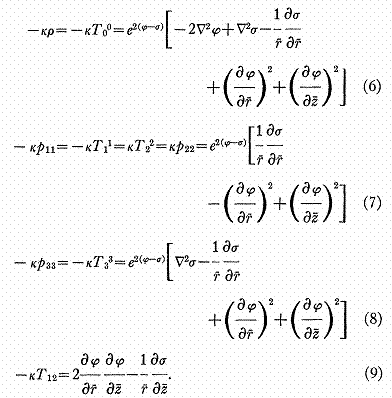
Le type de spécialisation impliqué par le choix de la métrique (1) apparaît clairement dans (7). La condition T12 fini, sur l’axe, impose que sur .

Sans perdre en généralité, nous pouvons poser sur

Si nous supposons qu’il n’y a pas de matière en , alors cette condition peut aussi être déduite de (5).

Nous pouvons maintenant construire un équivalent Newtonien de notre système, dans lequel

sont des coordonnées cylindriques polaires et dans lequel

est le potentiel gravitationnel (en unités gravitationnelles). Dans le vide il satisfait à l’équation de Laplace (2). Aussi longtemps qu’il est petit (3) et (4) impliquent que est du second ordre. L’équation (6) est alors, au premier ordre identique à l’équation de Poisson tandis que les équations (7), (8) et (9) impliquent que le facteur de « stress » dans le tenseur énergie impulsion est petit par rapport à l’énergie liée à la densité.

La signification de la condition de cohérence (5) est maintenant claire : La force gravitationnelle sur un corps entouré par un espace vide doit avoir une composante qui est nulle. Comme les autres composantes sont nulles par symétrie, (5) est simplement la condition d’équilibre Newtonienne. Nous pouvons maintenant considérer comme le potentiel Newtonien exact du système équivalent Newtonien bien que la densité du système Newtonien ne soit pas exactement la même que celle du système relativiste.

Comme l’équation de Laplace est linéaire, nous pouvons bien entendu superposer les solutions. En particulier, s’il y a deux corps [ par exemple, deux régions séparées dans lesquelles (2) ne s’applique pas ], alors les deux solutions correspondantes peuvent être superposées , à condition que (5) s’applique séparément pour chaque corps. Rappelons à toutes fins utiles quelques théorèmes de gravitation Newtonienne.

i) Si à et sauf dans une seule région fermée finie, alors la condition (5) est satisfaite.

ii) Si à et sauf dans une région fermée finie qui est totalement incluse entièrement dans la région et dans laquelle alors pour tout

iii) à et sauf dans deux régions fermées finies, l’une totalement incluse dans et l’autre dans et que dans chacune, est d’un signe, alors la condition (5) ne peut pas être satisfaite. Ce résultat important découle de (i) et (ii),. Si est coupé en deux parties 1 satisfaisant à l’équation de Laplace sauf dans le corps 1 et ² idem sauf pour le corps 2, alors la condition (5) pour le corps (1) exige que :

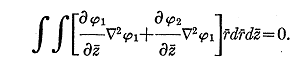
En vertu de (i) le premier terme s’annule, le second ne peut pas s’annuler en vertu de (ii). Le théorème montre qu’il n’y a pas de solution statique en relativité générale pour un problème à deux corps, constitués de types différents de matière associées à des masses de signe différents, localisées de chaque côté d’une surface définie par z = constante, avec une métrique tendant vers celle de Minkowski à l’infini.

Nous allons maintenant montrer que si on peut éliminer cette dernière condition, alors une telle solution devient possible.

3

La métrique uniformément accélérée

peut être transformée en celle de Weyl Levy-Civita (1) par la transformation

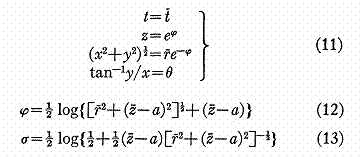
et a est une constante arbitraire. Ce que nous appellerons 0 satisfait l’équation de Laplace dans toute la partie concernée de l’espace, par exemple sur, , .

Comme nous l’avons vu avant, la métrique uniformément accélérée ne décrit qu’une partie de l’espace temps et la singularité à , ne doit pas nous surprendre.

Remarquons que pour ,

Considérons le problème à deux corps conformément à (iii), mais additionnons le potentiel 0 .

Cela implique que nous abandonnons la condition aux limites, que l’espace est Minkowskien à l’infini et que nous la remplaçons par une condition appropriée aux référentiels uniformément accéléré, dans un espace temps qui est plat à l’infini. Si chacun des corps est entièrement dans et si dans le corps (corps 1) dans la région de le plus faible , tandis que dans l’autre ( corps2) alors la condition (5) peut être satisfaite, dans les circonstances adéquates. Pour cela, à l’intérieur du corps 1, , et dans le corps 2 Comme , dans les deux régions, les signes ne sont plus des arguments qui interdisent une solution stationnaire.

Pour en établir la possibilité, nous allons procéder comme suit. Soit B1 et B2 deux régions finies d’espace avec B1 entièrement dans et B2 dans où Soit 1 solution de l’équation de Laplace partout à l’extérieur de B1, avec 1 --> 0 à l’infini, avec dans B1. De même soit 2 solution de l’équation de Laplace partout à l’extérieur de B2, et qui tend vers 0 à l’infini, mais avec dans B2. Ensuite considérons :

où a dans 0 est une constante et k, l sont des constantes à déterminer, avec l,k > 0 et Si la condition (5) est satisfaite pour B1 et B2 alors :

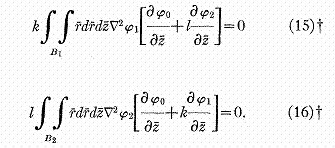
Comme le facteur k peut être ignoré dans (15), cette équation peut être considérée comme une équation déterminant l. De plus, comme dans B1

l va être positif. De même (16) détermine une valeur de k positive. Toutes les conditions du problème sont alors satisfaites ; et nous avons abouti dans la construction d’une solution du problème de deux corps de densité de masse de signe opposé uniformément accélérés.

Par exemple si nous pouvons prendre a=0 et

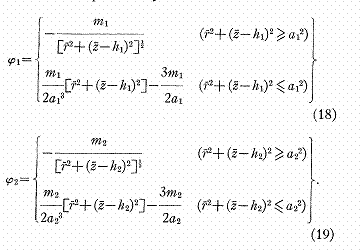
Ici par simplicité, h1 et h2 sont les paramètres plutôt que k et l.

La condition (16) devient, comme dans B2,

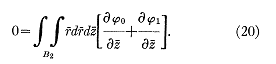
Si a2 << h2- h1, alors ceci devient en fait

Comme m1 est négatif.

De même nous devons avoir, si a1 << h2 - h1 et a1 << h1

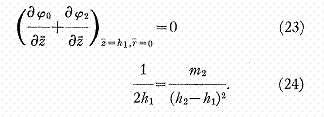
Il s’ensuit que dans les deux corps les dérivées de 0 sont du même ordre de grandeur que les dérivées des potentiels qu’ils produisent. Dans ce cas, les potentiels Newtoniens des deux corps sont petits, les dérivées de vont être petites au second ordre, malgré les termes additionnels dus à 0. En conséquence les densités sont d’un ordre de grandeur supérieur que les «  stress » , et sont elles mêmes, du premier ordre, donné par

De (12) et (13)

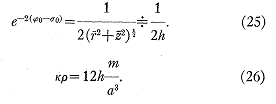
Il peut être intéressant de considérer le système dans le référentiel galiléen de départ à

[où]

Alors les corps apparaissent sous forme de sphères centrées à et de rayons Les densités sont toujours données par (26) et donc les masses sont , tandis que les accélérations sont

Dans la limite Newtonienne les accélérations auraient été données par

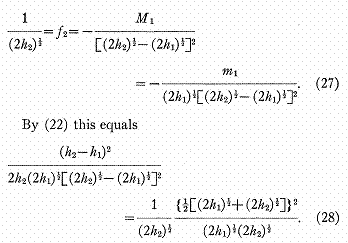
Ceci sera approximativement le cas, pourvu que h2 – h1 << h1

C'est-à-dire, pourvu que le produit de l’accélération et de la distance qui les sépare soit petit.

Ceci est une limitation appropriée pour le cas Newtonien. Il est intéressant de noter que les masses ne sont pas égales et opposées, mais ceci n’est pas surprenant puisque leurs accélérations doivent être différentes dans le modèle uniformément accéléré.

4

La métrique construite dans le chapitre précédent présente une singularité à

Ceci n’est pas surprenant , du fait que la métrique uniformément accélérée contient une telle singularité, qui est d’ailleurs purement artificielle et qui peut être éliminée en retournant à la métrique originale .Une telle élimination est elle possible également si nous avons

Remarquons d’abord que si , l’espace entier défini par correspond à z >= 0 dans et à un quart de l’espace temps ; dans Par les mêmes équations de transformation :

Nous avons maintenant la métrique

où la partie singulière de la métrique apparaît explicitement et où nous nous intéressons à seulement à z >= 0. Il est facile de voir que

est une fonction régulière de z et r. De plus, il est établi que pour, z petit, peut être développé en série de puissance de z² de coefficients dépendant de r, les coefficients eux-mêmes pouvant être développés en série de puissance de r² pour r petit. Remarquons que

est également de la même nature.

Définissons maintenant

nous arrivons à la métrique

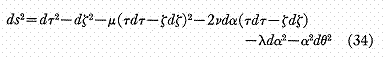
où les coefficients , sont des fonctions de seulement , Notons que cette métrique est invariante sous n’importe quelle transformation de Lorentz  , montrant que nous traitons bien le cas d’une accélération uniforme, bien que nous ne soyons plus dans un espace temps plat. Du fait de l’équation (33), la métrique (34) n’est valide que pour

Qu’arrive t’il sur, et au delà de cette frontière ?

La structure de ’34) montre clairement que cette frontière est délimitée par des parties de deux géodésiques de type lumière.

De plus, une comparaison laborieuse des coefficients permet d’évaluer les expressions de , à partir de et En considérant cette expression, on peut établir , en tenant compte du comportement de et de pour z petit comme sus mentionné, que les trois nouveaux coefficients peuvent être développés en série de puissance de , à proximité de la frontière, les coefficients des termes de cette série étant des fonctions de qui eux-mêmes peuvent être développés en puissances de ², au voisinage de =0. De ce fait la métrique est parfaitement régulière sur la frontière.

Comme la frontière est une géodésique de type lumière, la prolongation de la métrique au-delà n’est pas définie de façon unique. Il serait agréable de trouver une prolongation de la métrique (34) dépourvue de singularités et de matière, et qui recouvrerait tout l’espace temps.

La recherche d’une telle solution se heurte à de redoutables difficultés mathématiques et pour l’instant reste inaccessible. Un autre problème essentiel serait d’établir l’existence d’un tel prolongement de la métrique, malheureusement hors de portée pour l’instant.

Une solution d’un autre type a cependant été trouvée. Si on suppose que (34) conserve sa forme pour tout et , alors on peut obtenir une métrique qui est symétrique par rapport à = 0 et =0. Dans la région , les coefficients ne dépendent que de et sur la variable de type temps ( et de même sur tant que , l’image miroir des conditions va s’appliquer, c'est-à-dire qu’on va avoir deux corps de masses de signe opposé uniformément accélérés). La seule question, pour décider de la validité de ce type de solution est : Y a-t-il une métrique d’espace vide de ce type pour qui satisfait aux niveau de continuité que nous avons défini pour notre métrique précédemment obtenue pour Remarquons d’abord que la transformation

avec

génère la métrique

du moment que de (34) sont convenablement reliés aux

de (36). En fait il apparaît que les expressions pour en termes de sont identiques à celles en termes de et , si on remplace respectivement par

En conséquence, nous avons trouvé une métrique continûment compatible à notre métrique originale en prolongeant la métrique intermédiaire (34) au delà de la frontière.

Le comportement de (36) loin de la frontière est régi dans l’espace vide par les équations

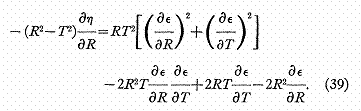
Comme (37) est une équation hyperbolique, nous n’aurons pas de singularités pour T>=0, R>=0, si et sont donnés en tant que fonction paires de R de façon non singulières à T=0. C’est bien le cas, du fait des propriétés de et de la relation de avec comme sus mentionné.

En fait au voisinage de T=0, peut être développé en puissance de T² avec des coefficients qui sont eux-mêmes développables en puissance de R², en vertu de la propriété correspondante de.

En conséquence sera non singulier. Comme pour , le seul doute au sujet du caractère non singulier provient du facteur R² - T².

Il est cependant facile de montrer que ce facteur ne conduit pas à une singularité pourvu que pour R=T, et ceci est une conséquence de (37) et du fait que = 0 pour R=T=0.

Nous avons abouti dans notre élaboration d’un solution, non singulière partout, des équations d’Einstein, correspondant au cas de paires accélérées de façon opposée chaque paire étant constituée de deux corps de masses de signe opposé.

[Notons que cette solution est très analogue à celle trouvée par Born dans le cas de l’électromagnétisme].

Comme T₀⁰ et m sont de même signe pour chaque corps, la masse négative que nous prenons en compte est celle de type (iv)