Effet catapulte : extrait de l’excellent livre « Astronomie et
Astrophysique » de Marc Seguin, Benoît
Villeneuve, chapitre 12, Compléments. Edité chez Masson )
Une sonde qui s'approche
d'une planète sur une orbite appropriée peut se servir du champ gravitationnel
de la planète pour accroître (ou diminuer) sa vitesse. Ce principe, appelé « effet catapulte », a
été exploité notamment par Voyager-2 lors de sa mission d'exploration des
quatre planètes géantes du système solaire. La sonde a utilisé chaque planète
pour augmenter sa vitesse et se propulser jusqu'à la planète suivante sans
avoir à brûler de carburant. Si les planètes étaient immobiles, l'effet
catapulte ne pourrait pas fonctionner: une sonde gagnerait de la vitesse en
s'approchant de la planète à cause de l'attraction gravitationnelle de
celle-ci, mais elle perdrait exactement ce qu'elle a gagné en s'éloignant de la
planète.
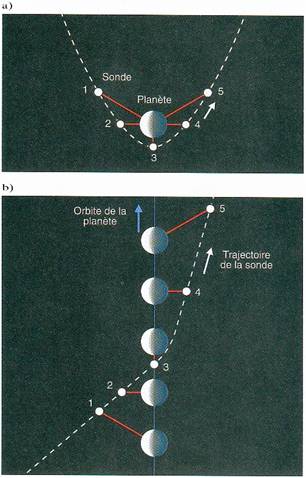
Figure 1 : a) La trajectoire d'une sonde d'après un observateur immobile par rapport à la planète.
b) La trajectoire de la même sonde d'après un observateur sidéral (immobile par rapport au Soleil).
Mais les planètes se
déplacent sur leur orbite, et leur gravitation entraîne les corps dans leur
voisinage. Ainsi, une sonde qui
s'approche d'une planète avec une vitesse moins grande que celle de la planète
verra sa vitesse s'accroître ( cf fig 1) ; en revanche, si la vitesse de la
sonde est plus grande que celle de la planète, la sonde perdra une partie de sa
vitesse.
Du point de vue d'un
observateur situé sur la planète, la sonde ne gagne ni ne perd d'énergie
cinétique: elle s'éloigne à la même vitesse qu'elle avait en s'approchant. Mais, si la situation est symétrique du point
de vue d'un observateur situé sur la planète, elle ne peut pas l'être du point
de vue d'un observateur «sidéral» immobile par rapport au Soleil. Examinons par exemple ce qui arrive à une
sonde lancée de la Terre vers Jupiter sur une orbite nécessitant le moins de
carburant possible (telle que nous l'avons définie au début de ce complément).
Lorsque la sonde arrive à l'orbite de Jupiter, on peut calculer qu'elle voyage à 7,3 km/s le long d'une trajectoire qui est presque parallèle à celle de Jupiter. Or, Jupiter voyage à 13 km/s le long de son orbite. Jupiter «rattrape» donc la sonde: pour un observateur sur Jupiter, la sonde se rapproche à 13 - 7,3 = 5,7 km/s.
Après que la planète et la
sonde se sont croisées, cette dernière s'éloigne à 5,7 km/s pour l'observateur
sur Jupiter (figure 2.a); mais, pour l'observateur sidéral, cela correspond à
13 + 5,7 = 18,7 km/s (figure 2.b): la sonde voyage 2,7 fois plus vite qu'avant! Le gain de vitesse (ici, 18,7 - 713 = 11,4
km/s) correspond au double de la
différence entre la vitesse de la sonde et la vitesse de la planète avant leur croisement. Du point de vue de l'observateur sidéral,
le gain d'énergie cinétique de la sonde se fait au détriment de l'énergie
cinétique de la planète. Dans le cas
d'une sonde dont la masse est de l'ordre de 1000 kg, la planète Jupiter voit sa
vitesse diminuer d'environ 10^-20 m/s.
Sur une durée de temps égale à l'âge de l'Univers (10 Ga), ce changement
entraîne une différence sur la distance totale parcourue par Jupiter de l'ordre
d'un millimètre !
Dans la plupart des cas, la
sonde qui s'approche de la planète n'est pas tout à fait sur une orbite
nécessitant le moins de carburant possible.
Elle croise alors l'orbite de la planète avec une certaine vitesse
radiale (perpendiculaire à l'orbite de la planète). Les calculs détaillés montrent que cette
vitesse n'est pas affectée, tandis que la composante de la vitesse de la sonde
le long de l'orbite de la planète (vitesse tangentielle) est modifiée selon la
règle que nous avons énoncée plus haut: le changement de vitesse tangentielle
correspond au double de la différence entre la vitesse tangentielle de la sonde
et la vitesse de la planète avant l'interaction entre la planète et la sonde.
.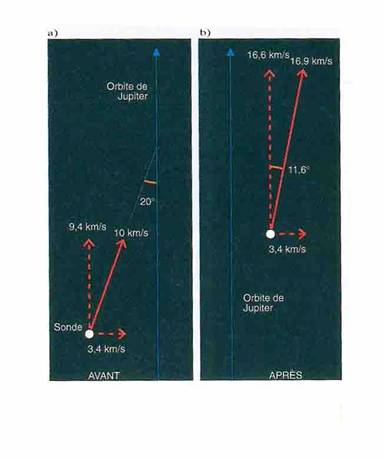
Figure 2 : Vitesse d’une sonde a) avant et b)
après son interaction avec Jupiter.
Exemple
Une sonde s'approche de
l'orbite de Jupiter à une vitesse de 10 km/s.
Du point de vue d'un observateur sidéral, sa trajectoire fait un angle
de 20° par rapport à l'orbite de la planète. Calculez la grandeur et la direction
de sa vitesse après son interaction avec le champ gravitationnel de Jupiter,
toujours du point de vue d'un observateur sidéral.
Solution
La composante de la vitesse
de la sonde perpendiculaire à l'orbite de Jupiter est 10 sin 20° = 3,4 km/s et
n'est pas affectée. La composante de la
vitesse de la sonde tangentielle à l'orbite de Jupiter est 10 cos 20° = 9,4
km/s. La vitesse de Jupiter le long de
son orbite est de 13 km/s. La sonde
gagne deux fois la différence entre ces deux vitesses: 2(13 - 9,4) = 7,2 km/s;
sa vitesse tangentielle finale est donc 9,4 + 7,2 = 16,6 km/s. Par le théorème de Pythagore, la grandeur de
la vitesse finale de la sonde égale = sqrt (3,4 ²+ 16,6²) = 16,9 km/s , et son
orientation par rapport à l'orbite de Jupiter équivaut à arctg (3,4/16,6) =
11,6° (figure 2).
NOTE :
L’effet catapulte a été utilisé la première fois en 1974 par la sonde
Mariner-10, qui se servit de la gravitation de Vénus pour modifier son orbite
et atteindre Mercure ( En fait, Mariner 10 se servit de Vénus pour freiner sa
course ; il s’agissait d’un effet « anti-catapulte »